- Про сайт
- Математика
- Теорія чисел
- Математичний аналіз
- Геометрія
- Комплексні числа
- Математика, 5 клас
- Інструкція щодо приєднання до свого класу на порталі NAUROK
- Завдання на 18 березня. Задачі практичного змісту
- Завдання на 19-20 березня
- Завдання на 23 березня
- Завдання на 24 березня. Частина від числа
- Завдання на 25 березня. Число за його частиною
- Завдання № 10 на 07 квітня Задачі про геометричні фігури
- Завдання № 11 на 09 квітня
- Завдання № 12 на 13 квітня. Середнє арифметичне
- Завдання № 13 на 15 квітня. Середнє арифметичне, задачі з N
- Завдання № 14 на 17 квітня. Відсотки 1
- Завдання № 15 на 22 квітня Режим конференції
- Завдання № 18 на 30 квітня - 4 травня. Два типи задач на відсотки
- Завдання № 21 на 8-11 травня. Відсотки та рівняння
- Завдання № 22 на 13 травня. Задачі на рух
- Завдання № 23 на 15-18 травня. Підготовка до контрольної роботи
- Завдання № 7 на 7 травня
- Завдання № 9 на 03 квітня. Задачі на рух
- Завдання №16 на 27 квітня Середнє арифметичне + відсотки
- Заняття № 19 на 6 травня. Два типи задач на відсотки
- Заняття № 25 26 травня 14-00. Підсумки 2019/2020 навчального року
- Заняття №17 на 29 квітня. Як знайти число за його відсотком?
- Контрольна робота № 5
- Куб із паперу
- Особливі випадки множення і ділення десяткових дробів 1
- Серія відеоуроків для 5 класу
- Тест 1 "Множення і ділення десяткових дробів"
- Математика, 6 клас
- 6 клас. Властивості пропорцій (вітамінна фейєрія)
- 6 клас. Контрольна робота №2.
- Властивості віднімання мішаних чисел
- Геометричне місце точок на координатній площині
- Додавання і віднімання звичайних дробів із різними знаменниками
- Додавання і віднімання мішаних чисел
- Домашнє завдання на 14 вересня 2020 року
- Ділення звичайних дробів
- Ділення звичайних дробів. Контрольна робота № 4. 6 клас.
- Задачі практичного змісту (звичайні дроби)
- Зведення звичайних дробів до спільного знаменника
- Знаходження дробу від числа
- Контрольна робота з теми "Звичайні дроби".
- Контрольна робота № 5. 6 клас.
- Множення звичайних дробів 2
- Множення звичайних дробів. 6 клас. Контрольна робота №3.
- Подільність чисел. 6 клас. Контрольна робота № 1.
- Порівняння звичайних дробів
- Порівняння раціональних чисел 6 клас
- Рівність звичайних дробів
- Самостійна робота 1, 04 грудня, тема "Відношення і пропорції"
- Самостійна робота 2, 11 грудня "Відношення і пропорції"
- Самостійна робота 3, 18 грудня, тема "Відношення і пропорції"
- Тема. Наближені обчислення
- Тема. Прямокутна система координат
- Тема: відношення і пропорції.
- Узагальнення знань із теми "Звичайні дроби"
- Число за частиною
- Тиждень математики і фізики в школі _2021
- Формули скороченого множення
- Методичні рекомендації щодо викладання математики в 2021/2022 н.р.
- Календарно-тематичне планування. Алгебра і початки аналізу, 11 клас. Профільний рівень.
- Календарно-тематичне планування. Алгебра і початки аналізу, 11 клас. Рівень стандарту.
- Календарно-тематичне планування. Геометрія, 11 клас. Профільний рівень.
- Календарно-тематичне планування. Геометрія, 11 клас. Рівень стандарту.
- Календарно-тематичне планування. Геометрія, 8 клас.
- Календарно-тематичне планування. Математика, 5 клас.
- Календарно-тематичне планування. Математика, 6 клас.
- Нові програми для 1-11 класів загальноосвітніх навчальних закладів з усіх предметів
- Розвантаження програм для учнів 10-11 класів
- Методика математики
- Розробки уроків
- Гімнастика для учнів під-час уроку (1-2 хв)
- Програма авторських курсів з методики викладання математики
- 30 фраз-мотиваторів замість "Неправильно"
- Вебінар майстер-клас
- Оцінка за ведення зошита з математики
- Поділ кола на рівні частини
- Про ДПА з математики у 2016 році
- Робота з обдарованими учнями
- Серпневі педагогічні зустрічі 2020
- Віодеролики для уроків
- Nature by numbers
- Історія математики
- Где доллар?
- Пролема вибору з точки зору теорії імовірності
- Четвертий вимір - наочне пояснення
- GIF-картинки, які пояснюють без слів
- GeoGebra
- Аналіз задач ЗНО
- Арифметичний квадратний корінь
- Графік лінійного рівняння
- Звичайні дроби і локшина для басейну
- Коло дев*яти точок та пряма Ейлера
- Навчальні відео Академії Салмана Хана
- Перерізи куба площиною і не тільки
- Терема Піфагора
- Тригонометричне коло
- Задачі
- Книги
- Алгебра. У роки. 9 клас. І семестр і ІІ семестр
- 100 задач оптимізації +70 задач бізнес-прогнозування
- Алгебра, 7 клас. Уроки
- Алгебра. 8 клас. Уроки
- Геометрія, 8 клас (авт. Єршової А.П. та ін.)
- Геометрія. Квести
- Електронні версії підручників
- Задачі з параметрами
- Комбінаторне, імовірнісне мислення та математична статистика
- Ланцюгові дроби. Арнольд В.І.
- Математика - це мова Всесвіту
- Математика за новою програмою. 5 клас
- Математика навколо нас
- Математика, 6 клас за новою програмою
- Математика. Біографії та портрети
- Математика. Квести
- О числе Пи. Жуков А.В.
- Основи теорії чисел. І.М. Виноградов
- Тригонометричні функції
- Математики говорять
- Олімпіади Конкурси
- 52 Міжнародна учнівська олімпіада з математики ІМО-2011
- 54 Міжнародна олімпіада з математики в Колумбії - перед змаганнями
- LIV Всеукраїнська олімпіада з математики
- V міський турнір юних математиків і фізиків
- І (шкільний) етап Всеукраїнських олімпіад з математики _2012
- І (шкільний) етап Всеукраїнських олімпіад з математики _2013
- І шкільний фізико-математичний турнір
- ІІ (міський) етап Всеукраїнської олімпіади з математики
- ІІ міський фізико-математичний турнір
- ІІ міський фізико-математичний турнір
- ІІІ (обласний) етап Всеукраїнських учнівських олімпіад з математики у 2012 році
- Вітаємо призера ІV етапу Всеукраїнської учнівської олімпіади з математики 2016
- Вітаємо призера ІV етапу Всеукраїнської учнівської олімпіади з математики 2017
- МАН
- І (міський) етап конкурсу-захисту робіт учнів-членів МАН України. 2014. Математика.
- Діофант, Διθφαητ
- Контрольна робота з математики І (міського) етапу конкурсу-захисту МАН 2018
- Контрольна робота з математики на І (міському) етапі МАН - 2012
- Контрольна робота з математики на І (міському) етапі МАН_2014
- МАН: деталі
- Учні
- Статті
- Комп’ютерна наочність на уроках геометрії
- Куб. Відстані між елементами.
- Метод ортогональної проекції
- Плач математика
- Площа перерізу многогранника
- Правильна чотирикутна піраміда
- Проведення уроків узагальнення та систематизації
- Суперматизм
- Укладання куль в евклідовому просторі
- Формування наукового світогляду на уроках математики засобами інформаційних технологій
- Числа футуризму
- Фільми про математику
- Math on-line
- Naціональний Математичний Вісник
- STEM-освіта
- Інтерактивні вправи
- Газета "Математика"
- Анонс № 1 (781), січень 2016
- Анонс № 12(816), 2017
- Анонс № 14 (794), липень 2016
- Анонс № 14(818), 2017
- Анонс № 15(819), 2017
- Анонс № 2 (782), січень 2016
- Анонс № 2 (830), 2018
- Анонс № 20(800), 2016
- Анонс № 24 (780), грудень 2015
- Анонс №12 (840), 2018
- Анонс №9 (837), 2018
- Педагогічне видання як провідник новацій у сфері освіти
- Слово редактора
- Геометрія. Квести
- Гурток для учнів 6-7 класів
- ЗНО з математики
- Мовою історичних фактів
- НМТ
- Обласний семінар-практикум
- Розподілені обчислення в Україні
A journey of a thousand miles begins with a single step…
Пропедевтика вивчення геометрії у 6 класі
Ндл, 03/04/2011 - 11:40 — Irina  Перше знайомство з геометрією відбувається у кожної людини по-різному, але в кожного це стається в перші ж годоини після народження. Немовля розуміє, що все на дотик має різну форму.
Перше знайомство з геометрією відбувається у кожної людини по-різному, але в кожного це стається в перші ж годоини після народження. Немовля розуміє, що все на дотик має різну форму.
Класифікація найпростіших геометричних фігур у початковій школі та життєвий досвід перших десяти років життя готує шестикласника до певних узагальнень.
Для роботи в цьому напрямі була створена (у 2002 році) комп*ютерна презентація про властивості геометричних фігур, найпростіші формули та їх застосування для учнів 6-го класу (у вкладенні).
- Додати коментар
- Читати далі
- 9005 переглядів
- Цитата
Тіла обертання
Ндл, 03/04/2011 - 11:16 — Irina
Для викладання стереометрії з використанням мультимедіа пропонується серія рисунків до задач, теорем чи інших ситуативних випадків взаємного розташування тіл обертання та многогранників, для практичного використання вчителів. PPT - у вкладенні.
- 2 коментаря
- Читати далі
- 11232 перегляди
- Цитата
Демонстраційні тести ЗНО
Ндл, 03/04/2011 - 10:22 — Irina Серед різноманітних інструментів підготовки до ЗНО 2011 з математики актуальним залишається посібник Особливістю цього посібника, принциповою рисою, яка відрізняє його від усіх інших, є те, що тренувальні тести згруповані у так звані Кроки - пари тестів, які розташовані у порядку зростання рівня їх складності.Крім того, посібник містить довідник з математики згідно з програмою ЗНО і, УВАГА!, демонстаційні тести! Це тести, що містять РОЗВ*ЯЗАННЯ усіх задач з поясненнями, схемами, графіками та рисунками. Розгляньте будову тесту, використайте його для самостійної роботи з послідуючою самоперевіркою - це найкорисніше - та приступайте до розв*язання решти тестів. Успіхів Вам.
Серед різноманітних інструментів підготовки до ЗНО 2011 з математики актуальним залишається посібник Особливістю цього посібника, принциповою рисою, яка відрізняє його від усіх інших, є те, що тренувальні тести згруповані у так звані Кроки - пари тестів, які розташовані у порядку зростання рівня їх складності.Крім того, посібник містить довідник з математики згідно з програмою ЗНО і, УВАГА!, демонстаційні тести! Це тести, що містять РОЗВ*ЯЗАННЯ усіх задач з поясненнями, схемами, графіками та рисунками. Розгляньте будову тесту, використайте його для самостійної роботи з послідуючою самоперевіркою - це найкорисніше - та приступайте до розв*язання решти тестів. Успіхів Вам.Демонстраційні тести № 1 та № 2 - у вкладенні.
- Додати коментар
- Читати далі
- 9570 переглядів
- Цитата
Microsoft Mathematics 4.0
Срд, 02/03/2011 - 20:00 — Irina являє собою графічний калькулятор, що будує двовимірні та тривимірні графіки, забезпечує покрокове розв'язання рівнянь, надає доступ до корисних інструментів, призначених для розв'язання математичних задач і задач з інших предметів.
Microsoft Mathematics 4.0 включає великий набір інструментів, засобів та інструкцій, створених з метою надання студентам допомоги у процесі розв'язання математичних та наукових завдань. Використовуючи дану програму учні мають нагоду навчитися розв'язувати рівняння крок за кроком, отримати кращі уявлення про основи алгебри, тригонометрії, математичних обчислень, фізики та хімії.
Microsoft Math доступний для завантаження абсолютно безкоштовно з 12 січня 2011 року за адресою Центру Завантажень Майкрософт:
- Додати коментар
- Читати далі
- 8812 переглядів
- Цитата
Властивості паралельного проектування
Срд, 19/01/2011 - 00:44 — IrinaЗавтра у 10-А відкритий урок з геометрії на тему "Властивості паралельного проектування". Конспектр уроку викладаю тут, для практичного використання вчителів та творчої адапції до конкретних умов різних класів.

Геометрія, 10 клас.
Тема. Властивості паралельного проектування та їх застосування до розв'язування задач.
.........................................
Мотивація навчальної діяльності у вивченні теми «Властивості паралельного проектування та їх застосування».
Художник малює картину, конструктор креслить креслення, фотограф фотографує, і водночас всі вони виконують одну справу - відображають просторові фігури на аркуші (площині). Процес відображення точок простору на площину називається проектуванням. Зображення, що отримується при проектуванні називається проекцією. Слово проекція виникло від латинського projection - кидання вперед, вдалину. Щось схоже на проекцію можна спостерігати, розглядаючи тінь, що відкидається предметом на поверхню стіни або підлоги при освітленні цього предмета джерелом світла.
Для правильного зображення на площині плоских геометричних фігур, розташованих у просторі, необхідно знати та вміти використовувати закони паралельного проектування. Жодне зображення на кресленні, на картині, тим більше - при фото чи кінозйомці не порушує цих законів. Повторимо їх сьогодні і ми та навчимося застосовувати для побудови рисунків до геометричних задач.
ВЕСЬ КОНСПЕКТ УРОКУ - У ВКЛАДЕННІ.
- Додати коментар
- Читати далі
- 15674 перегляди
- Цитата
Геометрія сфери та картографія
Ндл, 09/01/2011 - 20:44 — IrinaКартографія та її методи Картографічні проекції (рос. картографические проекции, англ. cartographic projections, нім. kartographische Projektionen) – способи зображення земного сфероїда на площині, при яких кожній точці М зображуваної поверхні відповідає точка М', яка назива-ється її зображенням на площині. Зв'язане з цим перетворення зображення неминуче приводить до спотворювань. Проте деякі характеристики картографічної сітки, нанесеної на поверхню глобуса, можуть бути збережені і на карті за рахунок інших характеристик, що піддадуться перекручуванню.

Картографічні проекції можна класифікувати по виду допоміжної геометричної поверхні, що може бути використана при її побудові. Візьмемо прозорий глобус з нанесеними на його поверхню лініями меридіанів і паралелей і крапкове джерело світла. Ми можемо укласти глобус (із джерелом світла, розташованим у центрі кулі) у циліндр. Задачею картографа є вибір проекції, що максимально відповідає задачам даної карти.
- Додати коментар
- Читати далі
- 4346 переглядів
- Цитата
Геометрія Рімана
Ндл, 09/01/2011 - 20:31 — Irina На площині Евкліда,так як і на площині Лобачевского, дві прямі можуть мати не більше однієї спільної точки, тоді як у сферичній геометрії, де роль прямих грають великі круги сфери, дві «прямі» завжди перетинаються у двох діаметрально протилежних точках сфери. Таким чином, у сферичн

ій геометрії не має місця одне із самих важливих положень геомеметрій Евкліда і Лобачевського про те, що через дві різні точки проходить лише одна пряма. Геометрія Рімана схожа з сферичною геометрією, але в ній присутнє вищенаведене положення геометрії Евкліда і Лобачевського.
В геометрії Рімана пряма визначається двома точками, площина - трьома точками, дві площини перетинаються по прямій. Ріман додав до числа аксіом слідуюче твердження: кожна пряма,яка лежить з даною прямою в одній площині, перетинає цю пряму. Це означає, що в геометрії Рімана зовсім відсутні паралельні прямі, а сума кутів будь-якого трикутника більше 1800. При цьому з'ясувалось, що площина Лобачевського є одним із окремих випадків ріманових площин.
Ріман, розвиваючи свою систему, ще сильніше змінив евклідову аксіоматику, ніж Лобачевський. Отже, запропоновані Ріманом ідеї та методи відкрили нові в розвитку математики й набули застосування в механіці та фізиці, зокрема в теорії відносності.
На застосуванні ріманової геометрії до побудови перспективи, створено новий напрямок у теорії зображень, що відбиває геометричні властивості психофізичного простору.
- Додати коментар
- Читати далі
- 9195 переглядів
- Цитата
Теорема про суму кутів трикутника та гносеологічна теорія Всесвіту
Ндл, 09/01/2011 - 02:58 — Irina  Кожний семикласник вивчає в школі геометрію Євкліда і знає, що сума кутів трикутника дорівнює 180 градусів. Проте, якщо трикутник розташувати на зовнішній поверхні сфери, то цю рівність буде порушено.
Кожний семикласник вивчає в школі геометрію Євкліда і знає, що сума кутів трикутника дорівнює 180 градусів. Проте, якщо трикутник розташувати на зовнішній поверхні сфери, то цю рівність буде порушено.
Першим вченим, що піддав сумніву універсальність геометрії Евкліда у масштабах Всесвіту, був М.І. Лобачевський.
Лобачевський виходив з того, що якщо реальний простір не можна повністю описати за допомогою законів Евклідової геометрії, то сума кутів трикутника, розташованого на небесній сфері, буде меншою за 180 градусів.
Вершини такого експериментального трикутника були вибрані Лобачевським там чином: одна вершина на Землі, друга - на Сонці, а третя на зірці Сіріус, сузір'я Великого Пса. Якщо б сума кутів цього трикутника виявилась меншою 180 градусів, то у неевклідової геометрії виникла б модель, краща за всі існуючі моделі - природа. Але сума кутів цього трикутника була меншою за 180 градусів на таку незначну величину, що не виходила за рамки допустимої похибки вимірювань.
- Додати коментар
- Читати далі
- 14011 переглядів
- Цитата
Псевдосфера
Ндл, 09/01/2011 - 02:31 — Irina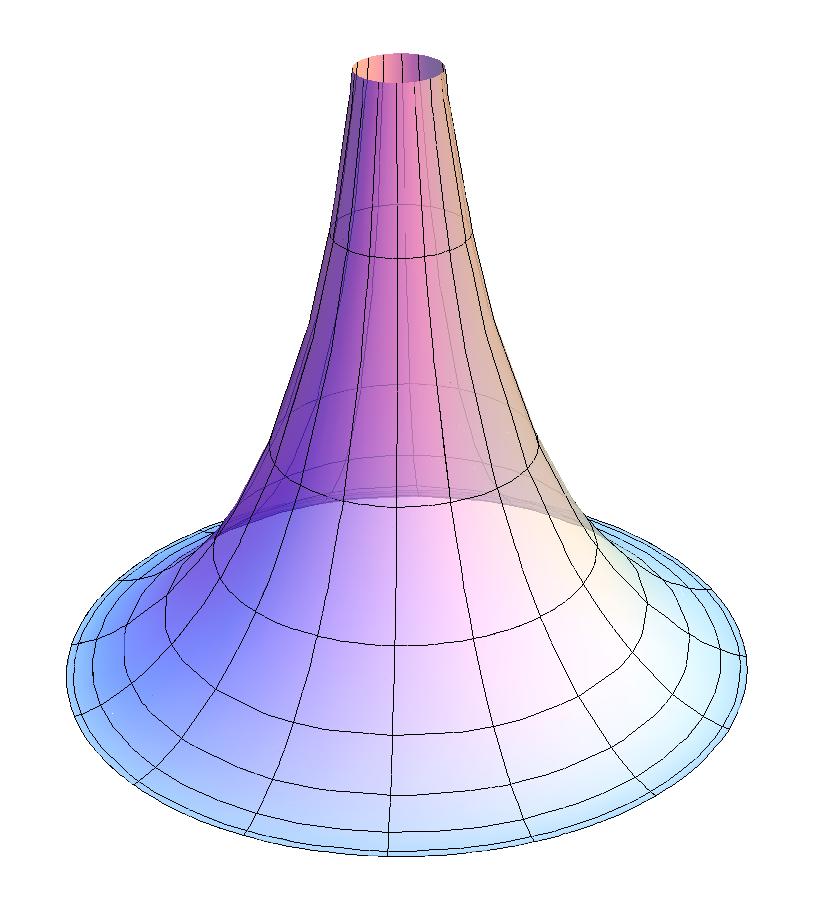
Коли дитина, що гуляє по тротуару, тягне візочок по дорозі, то візочок описує лінію , яка називається трактрисою (що означає «лінія ведення»).
Беручи границю тротуару, вздовж якої йде дитина, за вісь обертання і обертаючи навколо неї трактрису, ми дістанемо поверхню обертання . Цю поверхню називають псевдосферою. Вона має чудову властивість: якщо гнучка плівка щільно прилягає до якої-небудь частини цієї поверхні, то вона може ковзати по ній в якому завгодно напрямі не зморщуючись і не відстаючи від поверхні.
Для істот, які жили б на псевдосфері (на відміну від нас, які живуть на сфері) панували б закони не нашої звичайної евклідової геометрії, а закони неевклідової геометрії Лобачевского.
- Додати коментар
- Читати далі
- 4934 перегляди
- Цитата
Множення найрізноманітніших чисел
Чтв, 09/12/2010 - 21:40 — Irina - джерело великої кількості помилок учнів різного віку. Звичка користуватись калькулятором для підрахунків зіграла погану послугу всім, що не достатньо засвоїв класичного множення "в стопчик". А ЗНО та інші іспити передбачають заборону на користування калькулятором! Тут може згодитися цікава схема такого множення для кмітливих та уважних.
- джерело великої кількості помилок учнів різного віку. Звичка користуватись калькулятором для підрахунків зіграла погану послугу всім, що не достатньо засвоїв класичного множення "в стопчик". А ЗНО та інші іспити передбачають заборону на користування калькулятором! Тут може згодитися цікава схема такого множення для кмітливих та уважних.
- Додати коментар
- Читати далі
- 4205 переглядів
- Цитата
Діофант, Διθφαητ
Срд, 08/12/2010 - 22:50 — Irina Діофант – останній видатний математик античного світу. Про його життя майже нічого не відомо. Збереглася лише частина його праці «Арифметика», але саме вона була відправною точкою для теоретико-числових досліджень П.Ферма, Л. Ейлера, К Гаусса. Його ім’ям названо два великих розділи теорії чисел – теорія діофантових рівнянь та теорія діофантових наближень. Διθφαητ... Яка загадкова і яка харизматична постать! У цьому році для наукових досліджень була обрана теорія діофантових рівнянь.
Деталі - згодом.
- Додати коментар
- Читати далі
- 7787 переглядів
- Цитата
2=1. Математика и право. Софизмы в математике и в жизни. ;-)
Птн, 19/11/2010 - 00:40 — Irina2=1
...
 Учитель повернулся к доске и написал: а = b.
Учитель повернулся к доске и написал: а = b.
- Откуда вы знаете? - раздался с задней парты ломающийся голос отличника Гойскера.
- Откуда я знаю что?
- Что "а" равно "бэ".
- Прекрасный вопрос, - кисло сказал учитель. - Я не знаю. Но я допустил. Если вы заметили, я сказал: предположим, что "а" равно "бэ".
Дождавшись, когда ученики успокоятся, учитель продолжал:
- Умножаем обе части уравнения на "а". Получается...
Он написал: a x a = a х b, то есть a2 = ab. Класс молчал.
- Отнимаем от обеих частей уравнения "бэ"-квадрат, - сказал учитель и написал: a2 - b2 = ab - b2. Класс молчал.
- А теперь... - сказал учитель, не в силах сдержать счастливой улыбки, - кто может сказать, что мы теперь делаем?
- Идём домой смотреть хоккей, - сказал отличник Рабунский. - Он явно был сегодня в ударе.
- Правильно, - сказал учитель. - Но не сейчас. До конца урока ещё пятнадцать минут. А пока продолжим доказательство. Что у нас в левой части уравнения? Разность квадратов члена "а" и члена "бэ", правильно? Чему равна разность квадратов? Она равна произведению суммы членов на их разность. А что в правой части? Общий множитель "бэ", который мы выносим за скобки. Преобразуем уравнение. Получается...
Он написал: (a + b) (a - b) = b (a - b).
- Понятно?
- Сокращаем обе части уравнения на "а" минус "бэ", - прокричал он, перекрывая ликующий гогот. - Получается...
Он написал: a + b = b.
Гогот не стихал. Учитель продолжал писать, одновременно выкрикивая:
- Так как "а" и "бэ" равны, заменяем в левой части "а" на "бэ". Получатся...
Он написал: b + b = b, то есть 2b = b.
- Сокращаем на "бэ". Получается: 2 = 1...
- 8 коментарів
- Читати далі
- 9252 перегляди
- Цитата
Извлечение квадратного корня "вручную". Метод Герона.
Втр, 26/10/2010 - 23:42 — IrinaМетод Герона Для начала давайте научимся вычислять квадратный корень (т.е. решать простейшие квадратные уравнения) с помощью арифметических действий. был известен ещё в Древней Греции и приписывается Герону Александрийскому. Герон жил в I веке н.э. и описал в своих книгах закон отражения света, формулу вычисления площади треугольника по трём сторонам, многочисленные механизмы. Интересно, что и в наше время метод Герона используется некоторых вычислительных машинах (может быть, и в вашем калькуляторе!). Обратимся к тексту самого Герона. Он объясняет свой метод на примере: пусть надо найти корень из 720.
Так как 720 не имеет рационального корня, то возьмем корень с очень малой погрешностью следующим образом. Так как ближайший к 720 квадрат есть 729, и оно имеет корнем 27, поэтому разделим 720 на 27. Получается  .
. . Разделим результат на 2, получим
. Разделим результат на 2, получим  . Это и есть результат. Если возвести это число в квадрат, получим
. Это и есть результат. Если возвести это число в квадрат, получим  . Погрешность составляет 1/36 единицы. Но при желании погрешность может быть и меньшей. Для уменьшения величины погрешности процедуру следует проделать ещё и ещё раз с вновь полученой величиной. В нашем случае с числом
. Погрешность составляет 1/36 единицы. Но при желании погрешность может быть и меньшей. Для уменьшения величины погрешности процедуру следует проделать ещё и ещё раз с вновь полученой величиной. В нашем случае с числом  .
.
В этом тексте Герона содержатся три идеи:
1) как выбирать начальное приближение;
2) как производить уточнение;
3) процесс можно повторять (итерировать).
Начнём со второй идеи. Пусть нам надо вычислить  . Если выбранное нами приближение x0 меньше истинного значения корня, то число
. Если выбранное нами приближение x0 меньше истинного значения корня, то число  - больше, и наоборот.Поэтому их полусумма
- больше, и наоборот.Поэтому их полусумма  будет ближе к искомому корню, чем
будет ближе к искомому корню, чем  . Обозначим её за
. Обозначим её за  .
.
Теперь третья идея: если полученной точности нам недостаточно, то можно повторить весь процесс уточнения, начиная уже с величины  :
:  . Уточнения можно повторять и дальше, пока мы не достигнем нужной точности. Видим, что для достижения результата нужно проводить вычисления по одной и той же формуле. Такие однотипные вычисления называются итерациями. Если значение корня стремится к некоторому числу
. Уточнения можно повторять и дальше, пока мы не достигнем нужной точности. Видим, что для достижения результата нужно проводить вычисления по одной и той же формуле. Такие однотипные вычисления называются итерациями. Если значение корня стремится к некоторому числу  , то говорят, что итерационный процесс сходится к числу
, то говорят, что итерационный процесс сходится к числу  .
.
Наконец, первая идея: Герон предлагает выбирать в качестве  число с ближайшим к a квадратом. Но его можно выбирать и из каких-то других соображений. Более того, если вы выбрали x0>0 неудачно - далеко от корня, то процесс всё равно будет сходиться к корню, только потребуется больше шагов.
число с ближайшим к a квадратом. Но его можно выбирать и из каких-то других соображений. Более того, если вы выбрали x0>0 неудачно - далеко от корня, то процесс всё равно будет сходиться к корню, только потребуется больше шагов.
Замечательное замечание. Не трудно придумать аналог метода Герона для поиска кубических корней числа:
 .
.
- Додати коментар
- Читати далі
- 23799 переглядів
- Цитата
Доведення нерівностей
Сбт, 16/10/2010 - 12:45 — IrinaНа шкільній олімпіаді з математики серед завдань для учнів 10-х класів було і завдання на доведення нерівності.
Задача. Доведіть, що  .
.
Доведення. Аналіз умови. Нірвність мість дві змінні, що розміщені в умові нерівності симетрично ( заміна  на
на  призведе до такої ж нерівності). Отже, розвязками нерівності є множина пар чисел виду
призведе до такої ж нерівності). Отже, розвязками нерівності є множина пар чисел виду  . Це дозволяє підібрати кілька пар чисел для перевірки.
. Це дозволяє підібрати кілька пар чисел для перевірки.
Доведення проведемо так. Замінимо  на
на  та розглянемо нерівність з однією змінною
та розглянемо нерівність з однією змінною  та параметром
та параметром  :
:


 .
.
Обчислимо дискримінант відповідного квадратного рівняння 
 .
.
Очевидно, що  набуває лише недодатних значень.
набуває лише недодатних значень.
Якщо  ,
,  , то многочлен
, то многочлен  тотожно рівний многочлену
тотожно рівний многочлену  , який набуває лише невід"ємних значень, тому нерівність
, який набуває лише невід"ємних значень, тому нерівність  доведена.
доведена.
Для випадку від"ємного дискримінанта,  і нерівність
і нерівність  виконується для
виконується для  .
.
Отже, і нерівність  виконується для всіх значень
виконується для всіх значень  та
та  . Тому і
. Тому і  правильна для вісх значень
правильна для вісх значень  та
та  . Доведено.
. Доведено.
- Додати коментар
- Читати далі
- 21440 переглядів
- Цитата
Топ-15 фактів про математику
Срд, 06/10/2010 - 20:20 — Irina
- Перший факт у нашому списку – центиліон вважається найбільшим числом у світі, яке має назву.
- Італійські вчені з’ясували, що риби мають математичні здібності. Раніше було відомо, що ці створіння вміють відрізняти великі косяки від маленьких, але знайшовся доказ того, що вони можуть навіть підрахувати кількість риб, що плавають навколо. Щоправда, поки що лише до 4.
- Деякі тварини теж вміють рахувати, – це дельфіни та мавпи.
- Математика не знала знака “=” аж до 16 століття. Першим його застосував британський математик Роберт Рекорд...
- Додати коментар
- Читати далі
- 13002 перегляди
- Цитата
Рівняння сфери в задачах ЗНО
Ндл, 03/10/2010 - 18:26 — Irina
Задача. При яких значеннях параметра а рівняння  визначає сферу? Знайдіть: а) координати центра сфери; б) площу поверхні сфери; в) значення параметра а, при яких площина
визначає сферу? Знайдіть: а) координати центра сфери; б) площу поверхні сфери; в) значення параметра а, при яких площина  буде дотичною площиною до цієї сфери?
буде дотичною площиною до цієї сфери?
- Додати коментар
- Читати далі
- 7209 переглядів
- Цитата
Взаємно однозначна відповідність у задачах ЗНО
Ндл, 03/10/2010 - 18:07 — Irina
Встановіть взаємно однозначну відповідність між точками 1) - 7) та площинами А) - Г).
А) x=y;
Б) x=z;
В) y=z;
Г) y=0.
1) A(-1;2;6);
2) B(Π; 3,14; sin Π);
3) C(sin1; tg1; cos0);
4) D(0; 4; √16);
5) E(log32;1;log23);
6) F(log39; 0;2);
7)G(1/2; 0,5; 1/3).
- Додати коментар
- Читати далі
- 4622 перегляди
- Цитата
Вектори в задачах
Ндл, 03/10/2010 - 17:45 — Irina
Використаємо правило трикутника додаванння векторів для розвязування задач: АВ + ВС = АС.
Задача1. Відрізок АВ поділено точками С1, С2 і С2 на чотири рівні частини. Знайдіть ДОБУТОК кооординат точки В, якщо А(2; 5), а С3(3,5; 0,5).
Відповідь: -4.
- Додати коментар
- Читати далі
- 4363 перегляди
- Цитата
Формула Кардано
Чтв, 23/09/2010 - 23:19 — IrinaФормула Кардано
Если воспользоваться современным математическим языком и современной символикой, то вывод формулы Кардано может быть найден с помощью следующих в высшей степени элементарных соображений:
Пусть нам дано общее уравнение 3-й степени: (1)
(1)
Если положить  , то мы приведем уравнение (1) к виду
, то мы приведем уравнение (1) к виду (2)
(2)
где  ,
,  .
.
Введем новое неизвестное u с помощью равенства
 .
.
- Додати коментар
- Читати далі
- 5414 переглядів
- Цитата
Календарно-тематичне планування. Геометрія, 10 клас. Профільний рівень.
Срд, 15/09/2010 - 23:12 — Irina
Календарно-тематичне планування створено на основі програми, призначеної для організації навчання математики в класах математичного, фізичного та фізико-математичного профілів. Її реалізація дозволить забезпечити для учнів можливість зміни рівня навчання математики в 10-11 класах, оскільки в ній містяться ті ж самі теми та збережена така ж послідовність їх вивчення, що й у програмі рівня стандарту. Зміст навчального матеріалу доповнено, а перелік навчальних досягнень учнів конкретизовано і уточнено у відповідності до фізико-математичного та математичного профілів навчання.
Матеріали календарно-тематичного планування курсу геометрії , 10 клас, профільний рівень - у вкладенні.
- Додати коментар
- Читати далі
- 15325 переглядів
- Цитата
множення двоцифрових чисел, що закінчуються цифрою 5
Втр, 14/09/2010 - 20:22 — IrinaДивись!
- 1 коментар
- Читати далі
- 6374 перегляди
- Цитата
Календарно-тематичне планування. Алгебра і початки аналізу, 10 клас. Профільний рівень.
Ндл, 12/09/2010 - 21:49 — Irina

Календарно-тематичне планування створено на основі програми, призначеної для організації навчання математики в класах математичного, фізичного та фізико-математичного профілів. Її реалізація дозволить забезпечити для учнів можливість зміни рівня навчання математики в 10-11 класах, оскільки в ній містяться ті ж самі теми та збережена така ж послідовність їх вивчення, що й у програмі рівня стандарту. Зміст навчального матеріалу доповнено, а перелік навчальних досягнень учнів конкретизовано і уточнено у відповідності до фізико-математичного та математичного профілів навчання.
Матеріали календарно-тематичного планування курсу алгебри і початків аналізу, 10 клас, профільний рівень - у вкладенні.
- 5 коментарів
- Читати далі
- 16721 перегляд
- Цитата
Календарно-тематичне планування. Алгебра і початки аналізу, 10 клас. Академічний рівень.
Ндл, 05/09/2010 - 21:25 — IrinaНа основі відповідної програми для академічного рівня створено календарно-тематичне планування курсу алгебри і початків аналізу 10 класу, академічного рівня для практичної роботи вчителя.
Повний текст - у приєднаному файлі.
- 2 коментаря
- Читати далі
- 23114 переглядів
- Цитата
Календарно-тематичне планування. Геометрія, 10 клас. Академічний рівень.
Срд, 01/09/2010 - 22:49 — IrinaІз Інструктивно-методичного листа про вивчення математики у 2010-2011 році":
Академічний рівень. Мета навчання математики на академічному рівні полягає у забезпеченні загальноосвітньої підготовки з математики, необхідної для успішної самореалізації особистості у динамічному соціальному середовищі, її соціалізації і достатньої для вивчення профільних предметів, для успішної майбутньої професійної діяльності в тих сферах, де математика відіграє роль апарату, специфічного засобу для вивчення й аналізу закономірностей, реальних явищ і процесів. Змістове наповнення програми реалізує компетентнісний підхід до навчання, спрямований на формування системи відповідних знань, навичок, досвіду, здібностей і ставлення (відношення), яка дає змогу обґрунтовано судити про застосування математики в реальному житті, визначає готовність випускника школи до успішної діяльності в різних сферах.
Зміст навчання математики структуровано за темами двох навчальних курсів „Алгебра і початки аналізу" та „Геометрія" із зазначенням кількості годин на їх вивчення. Такий розподіл змісту і навчального часу є орієнтовним. Вчителям і авторам підручників надається право коригувати його залежно від прийнятої методичної концепції та конкретних навчальних ситуацій.
На основі відповідної програми для академічного рівня вивчення геометрії у вкладенні - календарно-тематичне планування курсу геометрії 10 класу, академічного рівня, для практичної роботи вчителя.
- Додати коментар
- Читати далі
- 26311 переглядів
- Цитата
Нові програми для 1-11 класів загальноосвітніх навчальних закладів з усіх предметів
Сбт, 28/08/2010 - 01:29 — Irina- Додати коментар
- Читати далі
- 23061 перегляд
- Цитата
Команда України на Міжнародній учнівській олімпіаді з математики 2010 року
Ндл, 22/08/2010 - 02:59 — IrinaЗ 1 по 14 липня 2010 року у столиці Республіки Казахстан, місті Астані, відбулась 51-а Міжнародна учнівська олімпіада з математики. У змаганнях юних математиків взяли участь 517 учасників (серед яких тільки 47 дівчат) з 97 країн світу, школярі віком від 15 до 19 років. Україну на змаганнях представляли переможці та призери ІV етапу Всеукраїнської учнівської олімпіади з математики, - учні Києво-Печерського ліцею «Лідер» №171 та Харківського фізико-математичного ліцею №27. Всі члени команди повернулись з нагородами: команда України здобула 1 золоту, 2 срібні та 3 бронзові медалі.

На фотографії:
Веклич Богдан (золота медаль)
Хрущов Тимур (срібна медаль)
Теплова Дар'я (бронзова медаль)
Лавинська Тетяна (бронзова медаль)
Жениленко В'ячеслав (бронзова медаль)
Чорний Максим (срібна медаль)
- Додати коментар
- Читати далі
- 4657 переглядів
- Цитата
Презентація програми
Срд, 18/08/2010 - 23:23 — IrinaПрезентація програми
- Додати коментар
- Читати далі
- 4716 переглядів
- Цитата
Використання ланцюгових дробів. Задача про провідники.
Втр, 17/08/2010 - 23:58 — IrinaЗадача. За допомогою довільної кількості одиничних опорів побудувати електричне коло , що має опір 10/7...
- Додати коментар
- Читати далі
- 4426 переглядів
- Цитата
Обчислення функцій за допомогою ланцюгового дробу
Пн, 16/08/2010 - 16:31 — IrinaОкрім степеневих рядів, при обчисленні елементарних функцій на ПК використовуються також ланцюгові дроби.
- Додати коментар
- Читати далі
- 4858 переглядів
- Цитата
Теорія чисел
Птн, 13/08/2010 - 03:12 — IrinaЛанцюгові дроби. Програма факультативного курсу для учнів 9 класу
Про природу числа. Відео
Вітрувіанська людина Леонардо да Вінчі
Це загадкове число П
"Золотий переріз". З чого все почалося
- 2 коментаря
- Читати далі
- 12655 переглядів
- Цитата

