Персональна сторінка вчителя математики Ірини Кирдей

     Супрематизм – найбільш скандальна та революційна течія у сучасному мистецтві. Вона стала титульною в межах культурного явища більш відомого як Авангард. На полотнах його представників відсутні образи упізнаваного реалістичного світу, натомість композиція малюнку вибудована за допомогою абстрактних геометричних фігур.

       Найвідомішою з таких картин є «Чорний квадрат» Казимира Малевича. Ім’я та творчість цього художника є своєрідною нульовою точкою супрематизму як напряму у живописі.

       За походженням Казамир Малевич був поляк, але на сторінках свого щоденника неодноразово писав що насправді є українцем. Він народився у Києві у 1878 році і дитинство та юність провів на території Вінниччини, Харківщини, Чернігівщини...

      Естетика та дизайн грошових купюр - справа честі кожної держави. Саме тому кожна валюта - цк перш за все витвір дизайнерського мистецтва. А от вироби з купюр - чистої води креатив!

    Крісті Малкофф - канадська художниця, яка дуже любить подорожувати. Вона навчалася в Коледжі мистецтва і дизайну Челсі, і отримала ступінь бакалавра образотворчих мистецтв в Інституті Емілі Карр у Ванкувері в 2005 році. В своїй серії під назвою «Шматочки грошей», Крісті вікористовує разнокольорові купюри  всего світу, складаючи їх в бездоганні геометричні фігури.

         Картографія та її методи Картографічні проекції (рос. картографические проекции, англ. cartographic projections, нім. kartographische Projektionen) – способи зображення земного сфероїда на площині, при яких кожній точці М зображуваної поверхні відповідає точка М', яка назива-ється її зображенням на площині. Зв'язане з цим перетворення зображення неминуче приводить до спотворювань. Проте деякі характеристики картографічної сітки, нанесеної на поверхню глобуса, можуть бути збережені і на карті за рахунок інших характеристик, що піддадуться перекручуванню.

         Картографічні проекції можна класифікувати по виду допоміжної геометричної поверхні, що може бути використана при її побудові. Візьмемо прозорий глобус з нанесеними на його поверхню лініями меридіанів і паралелей і крапкове джерело світла. Ми можемо укласти глобус (із джерелом світла, розташованим у центрі кулі) у циліндр. Задачею картографа є вибір проекції, що максимально відповідає задачам даної карти.

                На площині Евкліда,так як і на площині Лобачевского, дві прямі можуть мати не більше однієї спільної точки, тоді як у сферичній геометрії, де роль прямих грають великі круги сфери, дві «прямі» завжди перетинаються у двох діаметрально протилежних точках сфери. Таким чином, у сферичн

ій геометрії не має місця одне із самих важливих положень геомеметрій Евкліда і Лобачевського про те, що через дві різні точки проходить лише одна пряма. Геометрія Рімана схожа з сферичною геометрією, але в ній присутнє вищенаведене положення геометрії Евкліда і Лобачевського.
В геометрії Рімана пряма визначається двома точками, площина - трьома точками, дві площини перетинаються по прямій. Ріман додав до числа аксіом слідуюче твердження: кожна пряма,яка лежить з даною прямою в одній площині, перетинає цю пряму. Це означає, що в геометрії Рімана зовсім відсутні паралельні прямі, а сума кутів будь-якого трикутника більше 1800. При цьому з'ясувалось, що площина Лобачевського є одним із окремих випадків ріманових площин.
Ріман, розвиваючи свою систему, ще сильніше змінив евклідову аксіоматику, ніж Лобачевський. Отже, запропоновані Ріманом ідеї та методи відкрили нові в розвитку математики й набули застосування в механіці та фізиці, зокрема в теорії відносності.
На застосуванні ріманової геометрії до побудови перспективи, створено новий напрямок у теорії зображень, що відбиває геометричні властивості психофізичного простору.

       Кожний семикласник вивчає в школі геометрію Євкліда і знає, що сума кутів трикутника дорівнює 180 градусів. Проте, якщо трикутник розташувати на зовнішній поверхні сфери, то цю рівність буде порушено.

       Першим вченим, що піддав сумніву універсальність геометрії Евкліда у масштабах Всесвіту, був М.І. Лобачевський.

      Лобачевський виходив з того, що якщо реальний простір не можна повністю описати за допомогою законів Евклідової геометрії, то сума кутів трикутника, розташованого на небесній сфері, буде меншою за 180 градусів.

       Вершини такого експериментального трикутника були вибрані Лобачевським там чином: одна вершина на Землі, друга - на Сонці, а третя на зірці Сіріус, сузір'я Великого Пса. Якщо б сума кутів цього трикутника виявилась меншою 180 градусів, то у неевклідової геометрії виникла б модель, краща за всі існуючі моделі - природа. Але сума кутів цього трикутника була меншою за 180 градусів на таку незначну величину, що не виходила за рамки допустимої похибки вимірювань.

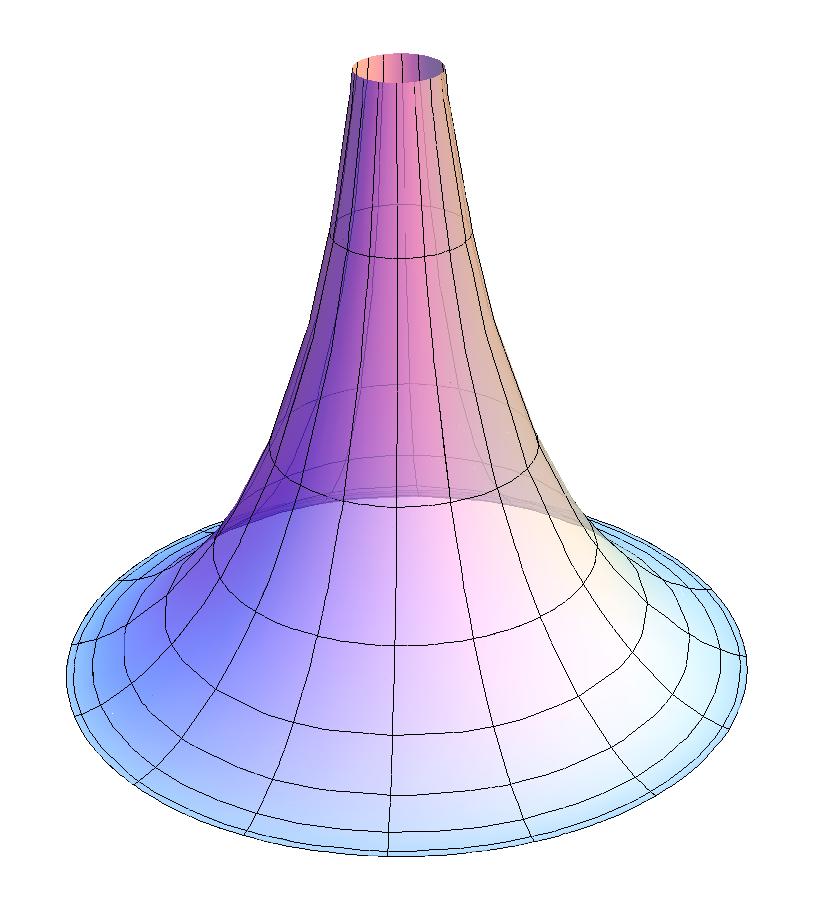
      Коли дитина, що гуляє по тротуару, тягне візочок по дорозі, то візочок описує лінію , яка називається трактрисою (що означає «лінія ведення»).
Беручи границю тротуару, вздовж якої йде дитина, за вісь обертання і обертаючи навколо неї трактрису, ми дістанемо поверхню обертання . Цю поверхню називають псевдосферою. Вона має чудову властивість: якщо гнучка плівка щільно прилягає до якої-небудь частини цієї поверхні, то вона може ковзати по ній в якому завгодно напрямі не зморщуючись і не відстаючи від поверхні.
Для істот, які жили б на псевдосфері (на відміну від нас, які живуть на сфері) панували б закони не нашої звичайної евклідової геометрії, а закони неевклідової геометрії Лобачевского.